算数オリンピックに関して、必要以上に神格化する必要もなければ、「絶対に参加するべき!」という立場でもありません。
ただし、ピグマリオンを学ぶことで、皆さんがチャレンジできるレベルにはなるかと思いますので、例えば小学3年生以下のキッズBEEにゲーム感覚で参加して、楽しい経験になるのであれば、お子さまにとってプラスの面が大きいのかと思います。
さて、今回は2020年の算数オリンピック(6年生以下)の問題をご紹介します。

2020年の算数オリンピックは、コロナ禍のため自宅受験。ファイナルなどが開催されなかった年でした。
その中で、第1問のこちらの問題は、正答率が90%を超える問題でしたし、低学年のお子さまでも取り組める問題です。
そう。神格化する必要はないのです。
特に、ピグマリオン学院でもMグレード(年長相当)から取り組む、魔方陣に慣れていれば、その変形のような問題なので、サッと解けるお子さまもいらっしゃるかと思います。
ピグマリオンでは、解法なども自ら創造することを重視しているので、以下の解説通りに考えなくても良いですが、代表的な考え方として、
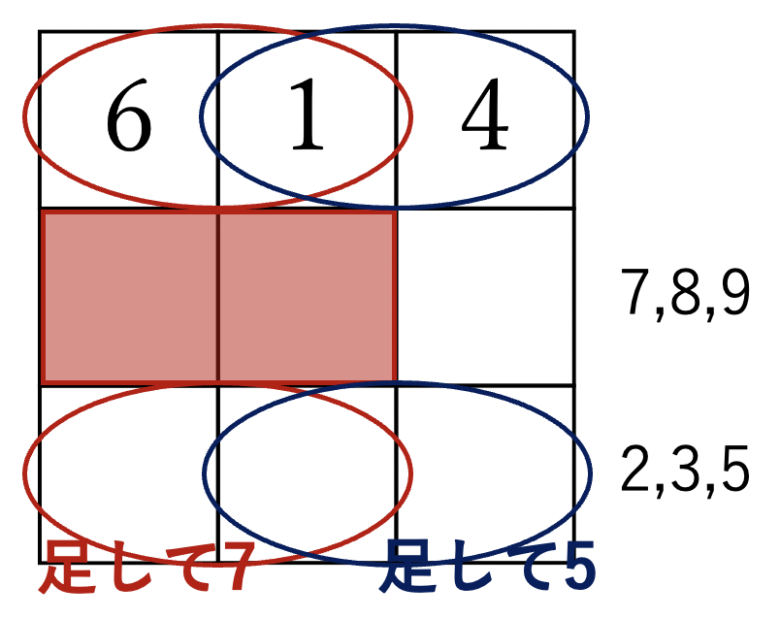
2×2マスの4つの和が全て等しいということであれば、中央の段の数が分からなくても、例えば赤枠や青枠で囲まれた箇所の数同士が一緒であることが分かります。
例えば、上段の左と真ん中が足して7であれば、中段の左と真ん中の数は重なっているので、下段の左と真ん中の数も足して7になります。
同様に、下段の青枠の数も足して5になるので、数の組み合わせは、下段の赤枠(5と2)、下段の青枠(3と2)になり、自然と真ん中の数は2になります。
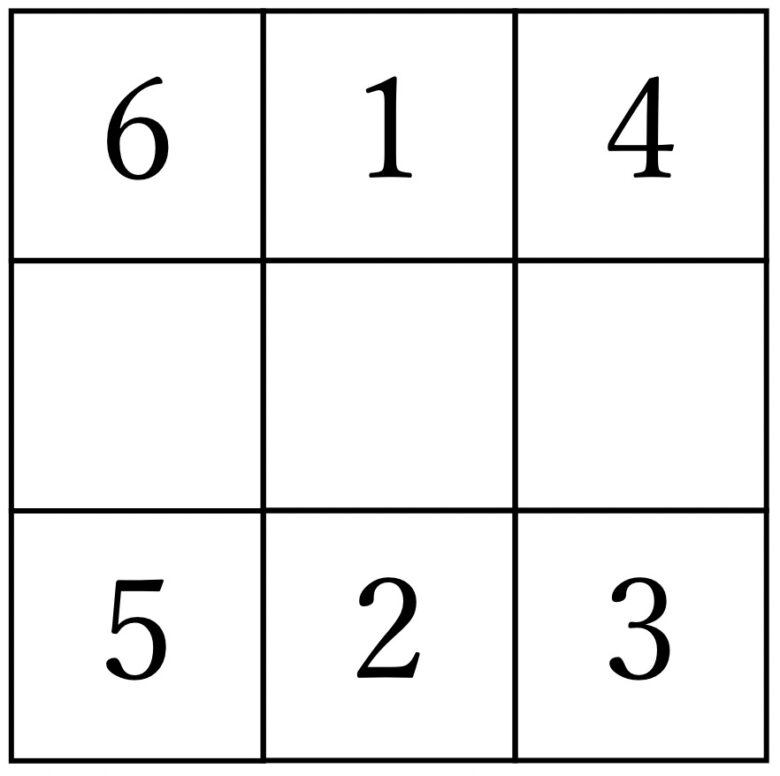
上段と下段の6つの数字が決まれば、あとは中段に7,8,9の数を埋めるだけ。
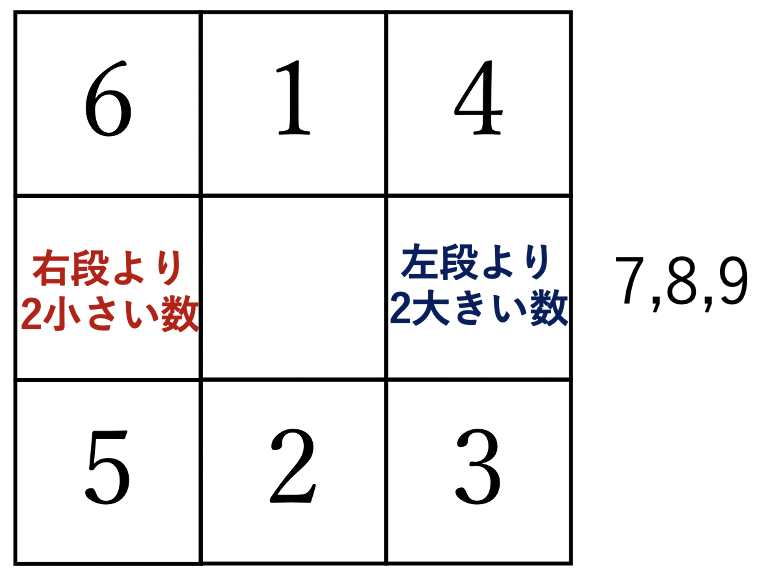
上の図の関係を確認すれば、中段の左側に7、右側に9が入ります。

ということで、算数オリンピックに出題される問題としては、かなり易しい問題になりますし、適当に数を当てはめていっても作業で解答に辿り着ける可能性のある問題です。
ただ、こういう問題は、高学年のお子さまが短時間でパッと解けるのも悪いことではないかとは思うのですが、むしろ低学年や中学年のお子さまが、少し時間をかけても良いので考えるのに適した問題だと感じています。
そして、魔方陣の解法を教えられて解けるようになったのではなく、自ら解法を創り上げたピグマリオンっ子にとっては、少しアレンジされたこちらの問題に取り組むのは、もし魔方陣を解くのがパターン化・マンネリ化しているようであれば、ちょうど良い刺激になり、改めて「考えることの楽しさ」を知る経験にもなるかと思います。
ピグマリオンには、イルソウレ学院などで算数や数学に対する先進的な取り組みがなされていますが、ピグマリオン学院 麻布十番教室でも、小学生向けの講習などで、このような楽しい問題にたくさんチャレンジする機会を作っていければと思います。
ピグマリオン学院 麻布十番教室

