前回の記事に続き、「つみきの数」について触れていきたいと思います。
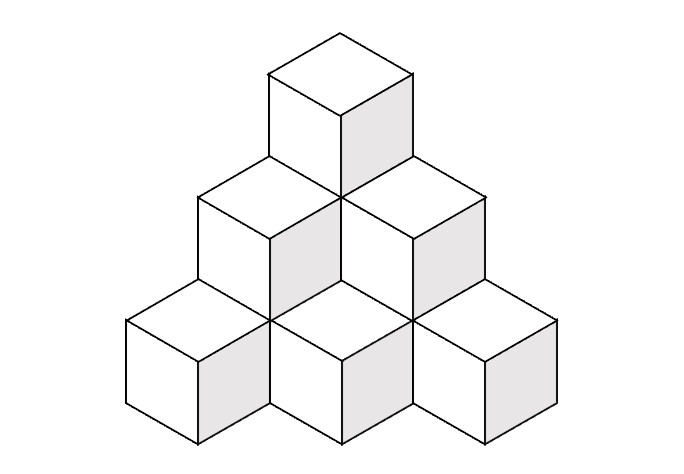
下の積み木は、6個と4個の合計10個の積み木ですが、それでは隠れている積み木の数を数えるためには、どうすれば良いでしょうか?
例えば、こぐま会さんの記事では、「印をつける」という考え方が推奨されています。
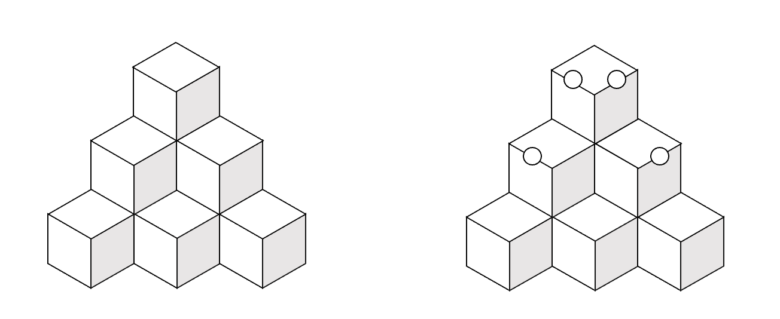
このように、みえない積み木に上に○をつけていくというやり方です。
しかし、私はこのやり方も、
「大人から子どもに一方的に解法を教えてしまっている」
と感じます。
例えば、ピグマリオンでは、ウッディブロックだけではなく、塗り絵や点描写などの取り組みをすることで、10まで数の概念を理解するころには、見えない積み木の数を自然と数えられる「3次元空間把握能力」が備わります。
いちいち、メモをしなくても、
どのように隠れているかを把握しているお子さまの方が圧倒的に多いです。
もし、
「印をつけないと数えられない」
お子さまの場合は、「○をつける」というようなメモやテクニックに頼るのではなく、「空間把握能力」そのものを養ってあげたほうが良いように思います。
例えば、
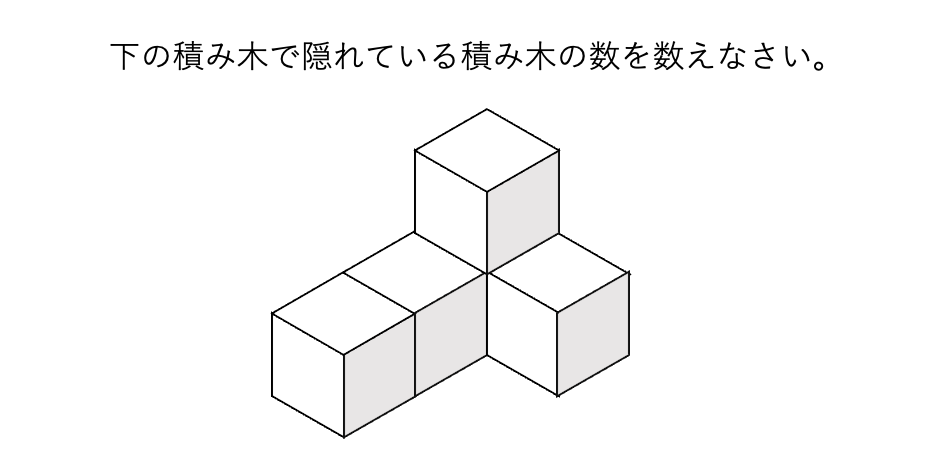
という問題であれば、何らかの知育に取り組んでいるご家庭のお子さまであれば、「1」と答えられる幼児は多いでしょう。
これは、「1個」のレベルであれば、隠れている積み木の数に対する「空間把握能力」があるからです。
そのため、前回の記事でも紹介したような、合成・分解を意識しながら学び続けると、
・全体と部分の関係を観る力
・合成分解能力
・同時に2つ以上のことを考える力
などが、養われていき、隠れている積み木が5個であろうと、10個であろうと、1個のレベルと同じような感覚で解けるようになっていきます。
…と、ここまで書いたところで、先ほど紹介した
「同時に2つ以上のことを考える力」
この力は、思考力の一つの基礎を構成していますが、この力をつけるには「試行錯誤」「トライアル & エラー」の経験が大切です。
少し脱線すると、「小学校受験の学習」だけしていると、この力が育ちにくいところがあります。
制限時間がある中で、素早く解くことを繰り返し、「考えずに解く」ことばかりすると、子どもが試行錯誤せずに、早急に「正解」を求めようとしていきます。
学校によっては、「ペーパー」の問題を工夫したり、「行動観察」「体操」「絵画・工作」の課題などで、二重課題のような課題をクリアできるか見極めようとしたりしていますが、それでも限界はありそうです。
このように、同じ問題に取り組むにしても、アプローチやその根底にある考え方が大きく異なること、前回と今回の記事で少しでも理解を深めていただければ嬉しく思います。
ピグマリオン学院 麻布十番教室

