さて、こちらの記事を読まれている方は、以下のような問題をご覧になったことはありますでしょうか?
円周率が3.05より大きいことを証明せよ。(東京大・2003)
すごくシンプルですが、誰もが習う円周率という身近なテーマを用いた入試問題で、20年前にもかなり話題になった問題です。
こちらの問題を普通に解こうとすると、どうしても高校数学の知識が必要になってはきますが、それでは、以下の問題であれば、いかがでしょうか?
円周率が3より大きいことを証明せよ。
この問題は、小学生が習うの算数の知識で解くことができます。
これ、わかりますか?
この場合、まず「円周と内接する正多角形の外周では、円の方が長くなる」という発想が思いつくかどうかから始まります。
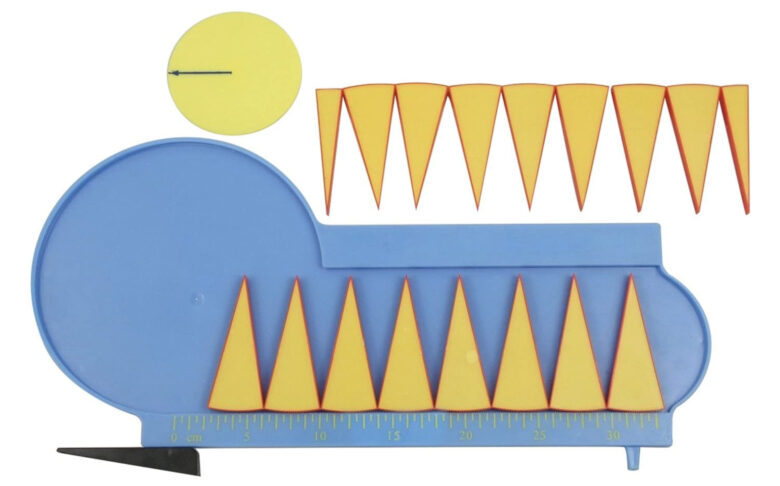
まずは、「直線よりも、曲線が長い」ということを理解しておきつつ、円の特徴を本質的に理解していたり、円周・円の面積説明器などに触れていれば、思いつきやすい発想です。
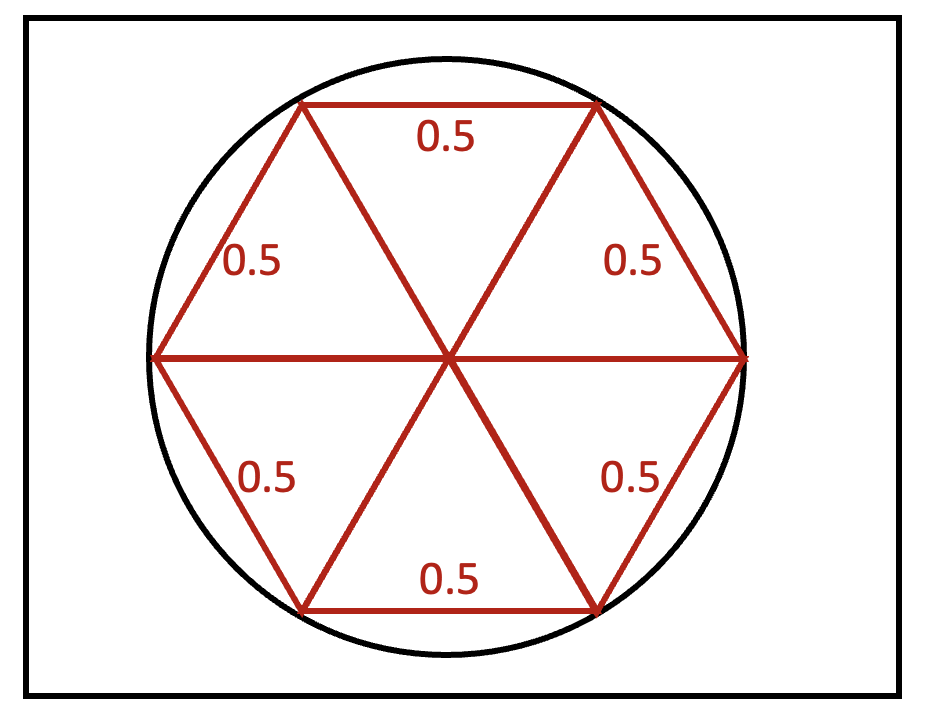
そして、正六角形で考えてみた時、下の円の直径を1と定義し、正三角形ができるように対角線を引くと、6つの正三角形ができます。この場合、下の円に内接する正三角形の一辺の長さは0.5(1/2)ずつになります。
これを利用すると、正六角形の外周は3となり、その外側にある円周は、3よりも長くなることがわかります。
東大の問題の場合は、この円周が3.05以上であることの証明になるため、正八角形や正十二角形などの外周を用いて回答する必要があり、その過程で高校数学の分野を用いますが、高校1年生で学ぶ余弦定理を用いれば解けるため、正六角形での解き方の考え方がわかっていれば、それほど難しくはありません。
このような問題を解く時、必要なのは計算力でしょうか?
そろばんやくもん式などで培った計算のスピードでしょうか?
フラッシュ暗算の能力が通用すると思いますか?
いえいえ。
この問題は、「円周率という定義」を根本的に理解する過程を省いたお子さまにとっては、難易度にしては苦手と感じる問題になるかと思います。
こちらの問題は、おそらく東大の数学の中では解き方もかなりシンプルな問題で、日頃から公式の暗記ではなく、「自分で考えながら問題を解く」という癖がついている人にとっては、かなり易しめな問題だったはずです。
その意味で、良問であり、認知度が高い東大数学の過去問になっているのです。
全ての問題が、このような傾向ではありません。
ただ、共通して言えることは、高校数学で重視されるのは「計算スピード」ではなく「計算力」でもなく、「図形形態能力」「空間認識能力」「数論理能力」なのです。
これは、ピグマリオンが幼児期から積み重ねようとしている力です。
「新しい問題に取り組む際に、自分で考える能力」を養っているのです。
これは、そろばんやくもんのような単純計算の反復では身につきにくく、むしろ無批判的に計算を続ける癖を続けていると、数学的思考力をスルーくせが身につく可能性が出てきます。
もちろん、そろばんやくもんを経験して数学で高得点を取ってきた方もたくさんいることでしょう。
ただし、その何倍も、そろばんやくもんを経験した後に、数学で挫折した方がいるはずです。
その背景には、「数を強化するベクトルを誤っている」ことにあるからです。
「計算=暗記」「計算=反復」
と刷り込みが入ると、数学が描く世界から遠のくリスクが高まります。
幼児期における暗記や反復の成功体験は、子どもよりも保護者が勘違いしてしまうリスクを高めます。
暗記力の優れた幼児期は、確かに大人が考えられないようなスピードで、覚えることができる場合がありますが、これが一生続くと勘違いしてしまうのです。
しかし、実態は逆で、当たり前ですが、高度な数学になればなるほど暗記では太刀打ちできなくなる問題の割合が増えてきます。
また、それ以上に大切なことは、暗記や反復の成功で、仮に受験に成功したとしても、それが社会人になってからの成功に結びつく確率が下がってしまうことです。
少しフォローするのであれば、暗記や反復の成功は、資格試験には強くなる可能性が高いです。
ただし、このような場合でも、同じ職業で「量よりも質」で要領良く学んできた人に、「仕事の質」で負けてしまう確率が上がることは、おそらくこちらの記事を読んでいる保護者の方であれば、想像がつくのではないでしょうか?
ピグマリオンをされるのであれば、そろばんやその他の計算メソッドに費やしている時間を、ぜひお子さまの、遊びの時間や社会科見学の時間、読書の時間、身体活動や芸術活動の時間に充てていただければと思います。
「二兎を追う者は一兎をも得ず 」
お子さまに、過度な負担をかけていませんか?
お子さまが混乱するような子育てになっていませんか?
私は、お子さまの前では、他の教室との併用についての強めの意見を控えるようにしています。
ただし、以上が私の本音の部分になります。
少し話が逸れましたが、幼少期や低学年のときに重宝されがちな計算力や計算スピード以上に大切な、高等数学にも太刀打ちできる数学的思考力を、小学校に入る前から養うメソッドがピグマリオンだと思っています。
その理由を、有名な東大の試験問題を例にして紹介させていただきました。
ピグマリオン学院 麻布十番教室

