さて、みなさんは小学校のときに学校で「はじきの公式」を習った記憶がありますでしょうか?
私は、うっすらですが学校で習った記憶があります。
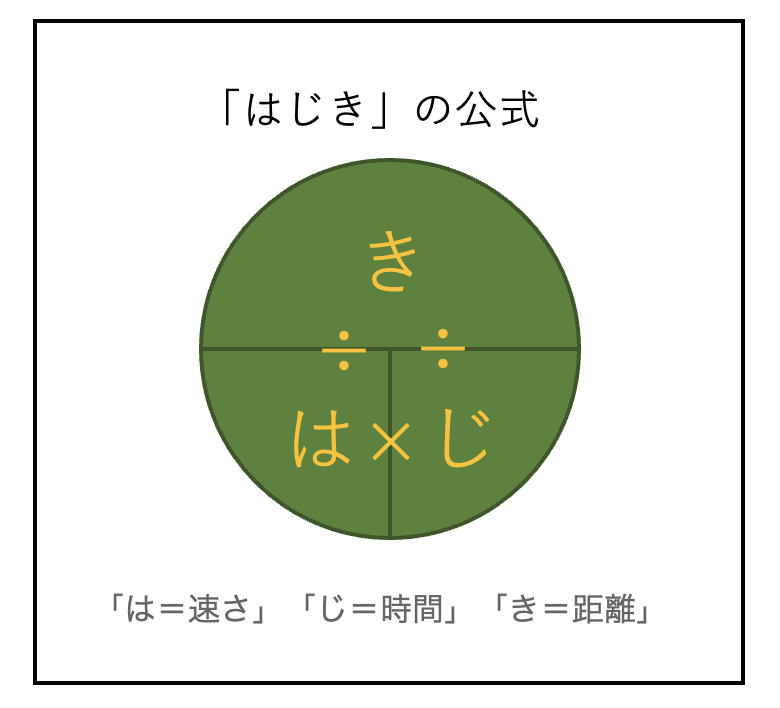
「速さ×時間=距離」「距離÷速さ=時間」「距離÷時間=速さ」を図式化して覚える方法ですが、これが塾の講師などからめっぽう評判が悪いのです。
私個人的にも、この考え方には共感ができるところが多々あります。
例えば、「時速20kmの自転車で2時間こいだら、40km進むんだ。そうか、マラソン選手って、こんなスピードで走っているんだな」というような具体的な体験が伴っていれば、このような公式を暗記しなくても、映像的な理解とともに、このような公式は理解できるはずです。
しかし、ではこういう先生に「かけ算九九を暗記してしまったら、思考力を失わないんですか?」と聞いたら、どういう答えが返ってくるのでしょうか?
「いやいや、九九は暗記して大丈夫です」
と言われてしまいそうです。
では、「はじきの公式」の暗記はダメで、「かけ算九九」の暗記が良い理由って、何かあるのでしょうか?
私は、ただ単にその講師が、「はじきの公式」を覚えなくても、「速さ」「時間」「距離」の関係性が理解できた一方、「九九は暗記した」という経験があったからだけなように思います。
ピグマリオンでは、「幼児期の九九の暗記は控えましょう」という指導をしています。
それは、「はじきの公式が思考力を奪う」というのと同じ理由で、
「かけ算九九の暗記が、本来かけ算ができるようになる過程で得られるはずの思考力や数量感を奪うから」
です。
「かけ算の本質」を理解し、「まとまりでとらえる能力」がつけば、暗記しなくても3桁×1桁くらいまでであれば素早く計算できるようになります。
では、かけ算の本質とは何なのでしょうか?
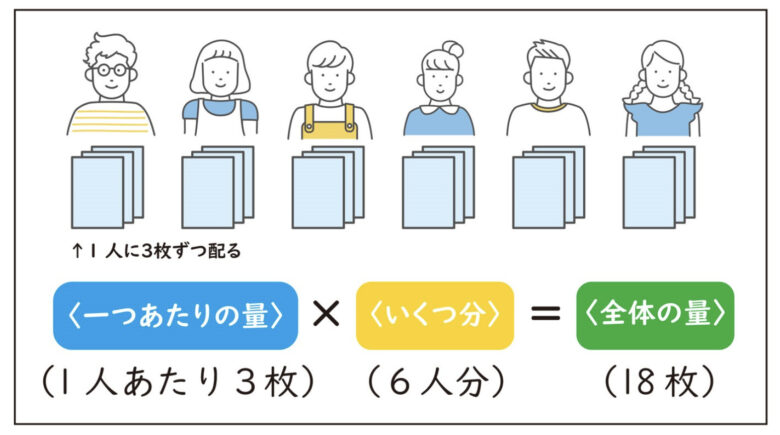
いくつかの説明ができるかと思いますが、例えば
「かけ算とは「〈一つあたりの量〉×〈いくつ分〉=〈全体の量〉」の形で全体の量を求める」
と説明することができるでしょう。
あるいは、面積算的な考えで、「かけ算とは四角形の面積を求めることと同じ。2つの数はタテとヨコの2辺で、その辺で作られる四角形のなかにある小さな正方形の数が面積になると考えればよい」
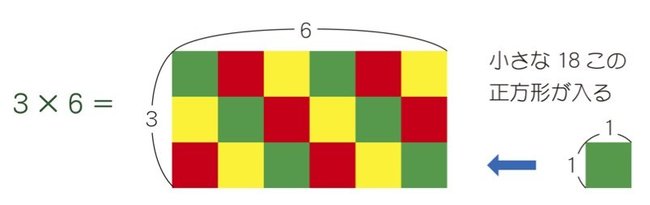
と説明することもできます。
数学は、測量の手段として発展してきた歴史があります。
「3+3+3+3+3+3=18」のように、足し算の延長だと考えることもできます。
しかし、幼児期の先取りで、例えば「さぶろくじゅうはち」という語呂や、「3×6=18」という文字列で暗記してしまうと、上記のような絵がイメージできず、かけ算の式の意味が理解できないまま表面的な進度だけが進んでいるお子さまが一定数います。
例えば、以下のような1000個の金ビーズを子どもに見せたとします。

「10というまとまりが、10列あって、それがさらに10段ある」とまでは言語化できなくても、実感として理解できている子は、「10と10と10で1000」だと答えられます。
しかし、幼児期の「かけ算九九」で暗記した子は、このような具体物を出されても、すぐに式や答えが出て来ないのです。
これ、「くもん算数経験者でピグマリオンを始めたお子さま」で良く起きる現象です。目の敵にしているのではなく、本当に良くこのような事態になるのです。
どういうことか?
子どもは「今はかけ算のレッスンだから、出てくる問題は全部かけ算だ」と考えて、与えられた数を覚えている九九になんとなく当てはめて計算して、「かけ算がわかった」と誤解します。
保護者も同様に「順調にかけ算を覚えてくれている」と勘違いしてしまうのです。
しかし、現実は81種類の「文字列の暗記」で途絶えてしまっている子が多い。
本質を理解せずに、ただ「パターンを暗記している」だけのケースが多いのです。
さて、これって「はじきの公式」と同じ現象が起きていると思いませんか?
ピグマリオンでは、2-3歳の頃から、ウッディブロックやヌマーカステンを使って「まとまりで捉える」という能力を段階的に高めていきます。
ヌマーカステンでは5までの単位、ドット棒Cでは10までの単位を意識しつつ、10000までの加減計算が暗算でできるようになります。
同時に長さやかさや時間の単位を学ぶことで、さらに「さまざまな種類のまとまり」が捉えられるようになったところで、かけ算の学びを実施しています。
だから、「実感を伴ったかけ算的思考」をもとに、10の段から、5→1→2→9→3→4→6→7→8と学び、学ぶ過程では、「4×7と24×7が同じタイミングで解ける」ようになります。
かけ算を習い始めて1ヶ月以内で、以下のような問題ができるようになります。

そして、より大切なことは、
「計算が解けるようになること」
ではなく、
「九九に頼らなくても、かけ算ができる数量感や図形感、そもそもの考え方が身についていること」
なのです。
暗記算数、暗記数学は、努力と忍耐次第では「受験」を乗り越えられる人もいますし、私たち大人は九九でかけ算を覚えてきて、その延長で育ってきています。
ただし、暗記算数、暗記数学は「根性論勝負」な側面が強く、「能力を伸ばす」ことには必ずしも直結しません。
「忍耐力を鍛える」のであれば、別に算数や数学でなくて良いはずです。
例えば、「tanの加法定理は、sin/cosで求まる」を学ぶときに、文字列の暗記を頑張るのではなく、
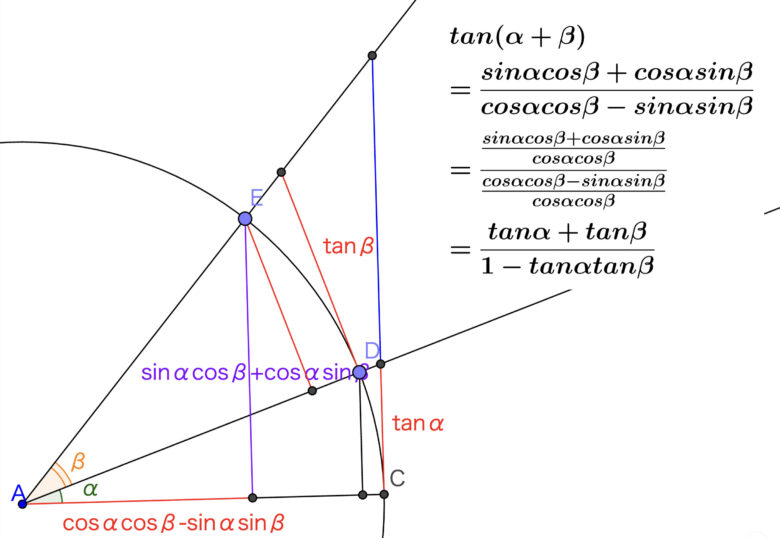
サッとこのようなイメージが出てくる方が、数学で苦労しなさそうではありませんか?
そう。数学が苦手なお子さまの一定数は、この「図的なイメージ」「絵的なイメージ」ができていないのです。
具体的なイメージができないから「数学が嫌い」になるのです。
いちいち、全て文字列で暗記しますか?
まだまだ、教育の世界では、「暑くても、喉が渇いていても、水を飲むな」的な悪しき体育会的な手法が多く残っています。
私たちの成功体験は、子どものために活かせる部分はあっても、より活かせる考え方ややり方はあると思います。
だからこそ、大人のやり方を押し付けず、他のご家庭の成功体験を参考にして、ピグマリオンはその成功ノウハウの宝庫なのですから、それを信じて取り組んでいただけると嬉しいです。
ピグマリオン学院 麻布十番教室
