今回は、慶應中等部の2011年の問題について解説しながら、いかにテクニックで解こうとすることが、そのお子さまの思考力を阻害するのかを考えてみたいと思います。
まずは、問題のご紹介。こちらの問題は、6年生ならば2問合わせて3分くらいで解答して欲しい問題です。
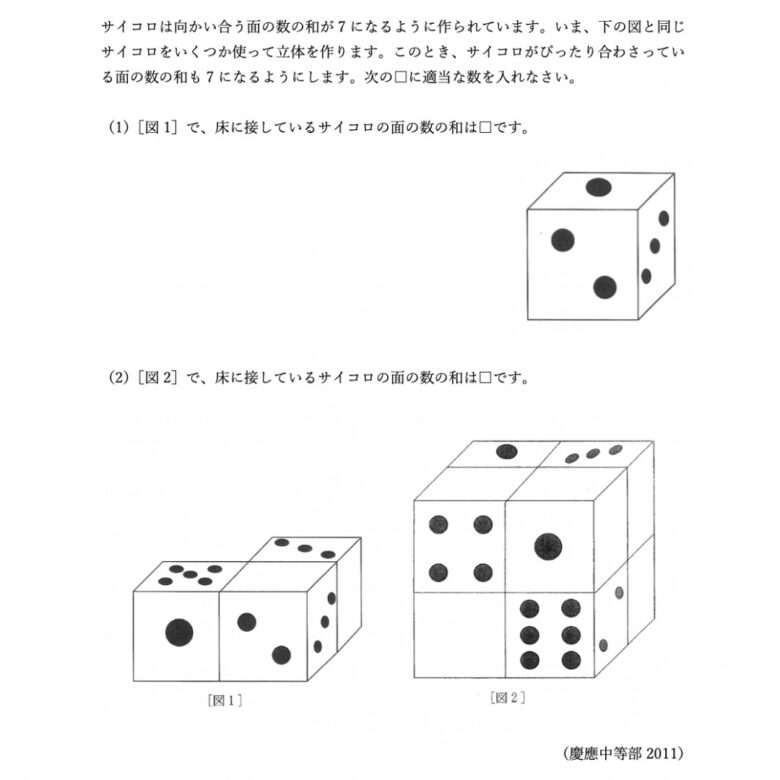
なお、第12回の算数オリンピック・キッズBEE(小学3年生以下対象)の類題よりは簡単な問題なため、小学低学年のお子さまでもチャレンジできる問題です。
さて、(1)の問題は、すぐに解けます。
左側手前の下(床への接面)は2、右側手前の下は6、右側奥の下は4で、合わせて12。
こちらは、おそらく正答率90%以上の問題で解説不要かと思います。
慶應中等部は問題の難易度自体はそれほど難しくなく、このような基礎的な問題も多い学校ではあります。
そして、(2)の問題なのですが、ピグマリオンでさいころコロコロや五方向知覚に慣れており、同時にナンバープレイスのようなパズル問題が大好きなお子さまであれば、こちらもそれほど時間をかけなくて解答できる問題なのではないでしょうか?
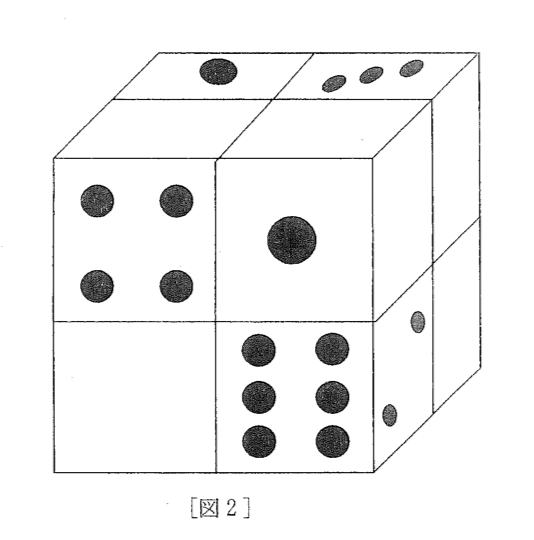
ピッタリ合わさっている面の和が7ということから、左奥(上のサイコロの上面が1)のサイコロの床面が6であり、右奥のサイコロの床面が4であることは、瞬時にわかります。
その後は、右下手前のサイコロから推理を進め、奥に1、右に2と配置されているところから、図1を見ながら頭の中でサイコロを回せば、右下手前の床面が3であることがすぐにわかります。
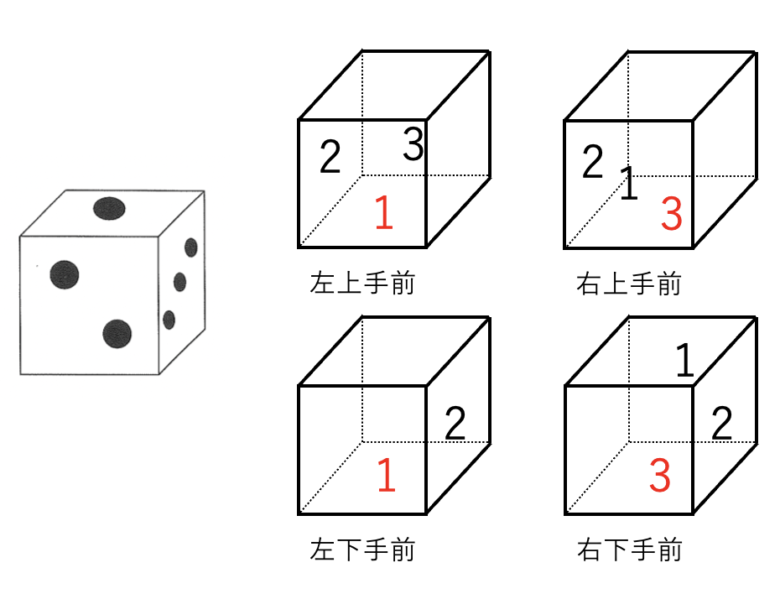
その次に、右上手前のサイコロを見ると、手前が1で下が3(右下手前の下面が3で上面が4のため)であることから、左面が2であることがわかります。
そして、左上手前の奥が3、左が2であることがわかるので、頭の中でサイコロを回し下面が1。
そうなれば、左下手前の床面も1であることがわかります。
奥の2つの床面が合わせて10、手前が3と1ということから、(2)の解答は14になります。
こちらの問題を解答する際に、「サイコロを潰して考える」という解説をしているサイトがありますが、こちらは時間がかかり過ぎて、実践的ではありません。
筑駒中の解説の記事でも書きましたが、図形感も育ちません。
https://www.chugakujuken.jp/tyuutoubu/sansu/gouhi_sansu/2011_gouhi_sansu/2/
他社批判になってしまい申し訳ありませんが、「慶應中等部に合格したい」と思われる受験生がこちらの解法でしか解けないのであれば、45分で20問近く解答しなければいけない中で、おそらく他の問題を解答する時間が削られ、不合格の可能性が高まるでしょう。
また、こちらの解説で良くないのは、「1・2・3は反時計回りに配置される」という説明書きがありますが、丸暗記を促すような解説であると同時に、誤った情報です。
一般的に、「1・2・3は反時計回りに配置される」サイコロが世の中に多いのは事実ですが、世の中には「1・2・3が時計回りに配置される」サイコロもあります。
あえて、このような丸暗記をしてきて自身で考えることを放棄するような受験生を避けるために、「1・2・3が時計回りに配置される」サイコロでの出題を考える先生もいらっしゃるかもしれません。
ネット情報であれ、塾の解説であれ、例え熟練の先生が解説していたとしても、間違っている可能性はゼロではありません。
やはり大切なのは「自分自身で考えること」。
ですね。
ピグマリオン学院 麻布十番教室


