「つみきの数」については、小学校受験でも頻出問題のため、さまざまな小学校受験塾でも授業で取り扱われています。
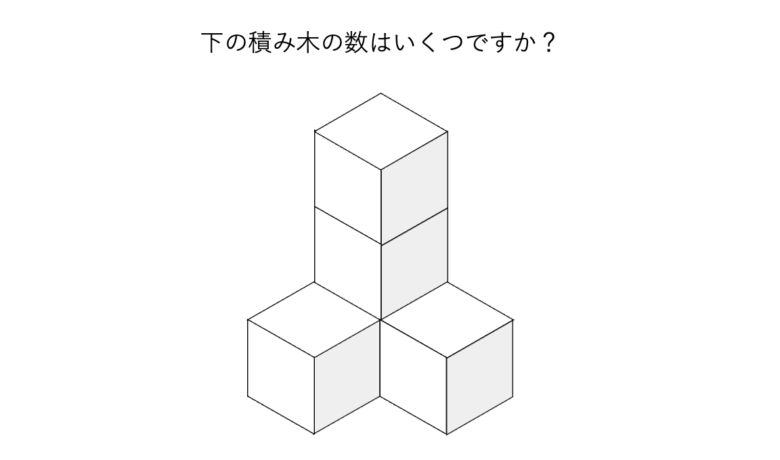
上記の問題は、ピグマリオン学院でも年少から取り組むレベルではありますが、皆様であればどう解くでしょうか?
このような問題が出題されたとき、例えば小学校受験塾では、「串を刺しましょう」などという指導がされたりします。
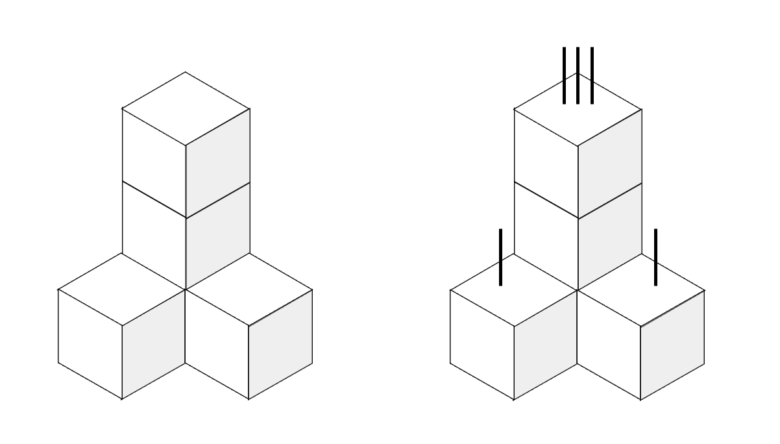
では、このような「串刺し解法」を幼児に「教える」ことは適切だと言えるでしょうか?
まず、「解法を教える」ということ自体が、ピグマリオンでは原則的にしないことなので、その時点で適切ではない(こどもの思考力を奪う)という考えではありますが、それ以外にも、
1. 単なるテクニック的な手法のため、思考力の基礎である構成把握能力が育つやり方ではない
2. 一直線的な思考のクセが強まり、多面的に思考する習慣から離れていってしまう
3. そもそも、解法として時間がかかり、ミスを誘発する可能性がある
4. テクニックで解けた成功体験が、その後の成長を阻害する可能性がある
などの弊害を、指導の現場にいて感じます。
そもそも「串刺し解法」は、時間がかかる解答手段であり、積み木の数が増えるとミスが起きやすいアプローチです。
例えば、
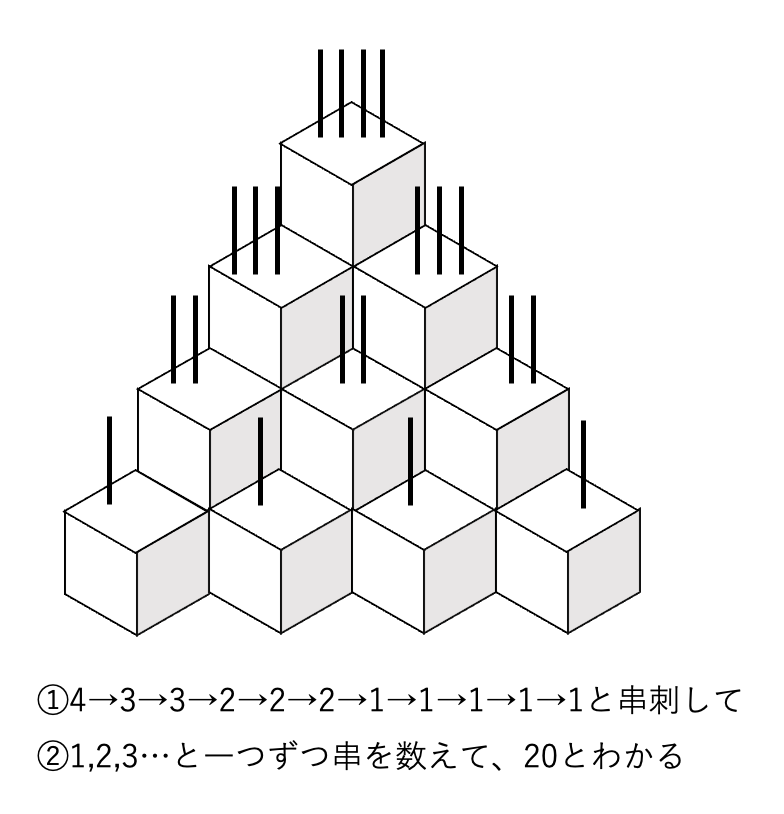
上記の解答手順として、①一つ一つに串を刺す記入をする、②記入した串の数を後から数える、③数えた数を解答欄に数字または○を記入する、という3段階の作業が発生します。
上の例のように積み木が5個くらいであれば、串を5つ刺せば良いですが、積み木の数が20近くなった場合、作業量が増え、3つのそれぞれの段階でミスが発生しやすくなります。
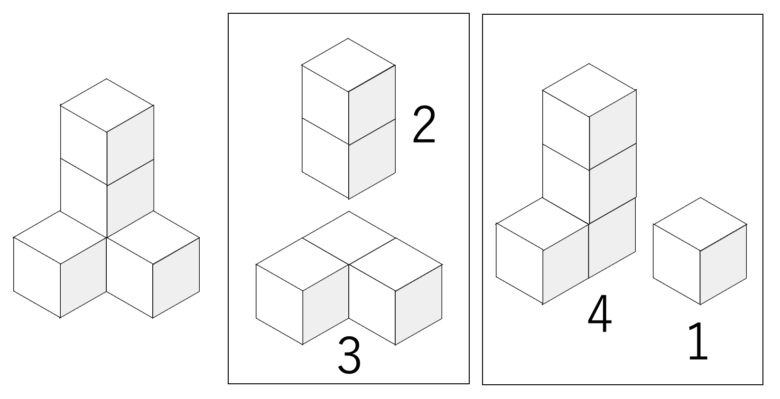
一方、3や4という小さい数の時から「まとまり」で考える癖がついており、大きい数については合成・分解などを通じて考える癖がついているピグマリオンのお子さまは、
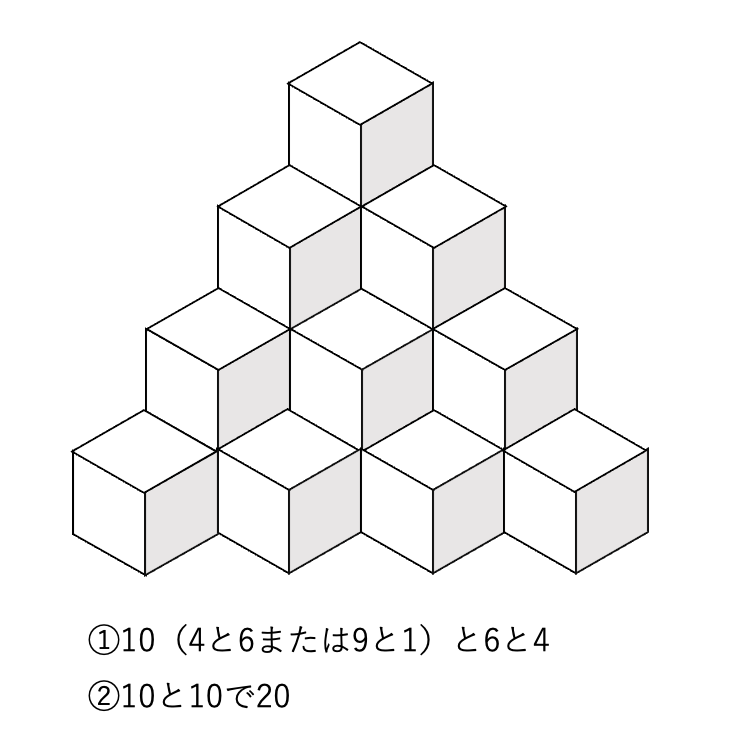
①瞬時に「3」と「2」で5と捉える(または、「4」と「1」で5と捉える)
②捉えた数を解答欄に数字または○を記入する
という手順で、時間も短く、ミスも起きにくいやり方を、自ら習得しています。
この延長線上で10個までの積み木、20個までの積み木と取り組めば、ブロックが20個近くなっても、同じように素早く正確に解答できます。
「瞬時に捉える」という状態は、「立体構造そのものを数や量として捉えられている状態」です。
合成・分解を通じて解答できるお子さまは「ながら作業」でも答えを導き出せると思います。
例えば食事をしている時にこちらの問題をモニターで出されたとしても「瞬時に」積み木の数を数えることができるでしょう。
一方「串刺し解法」のお子さまは、同じような場面で解こうとした場合、積み木を一つ一つ数えて解答に辿り着かなければいけないため、仮に解けたとしても時間がかかるのは容易に想像がつくのではないでしょうか?
では、どちらのお子さまの「立体把握能力」が育っていると思いますか?
答えるまでもありません。
仮に同じ問題を解けたとしても、「串刺し解法」のお子さまと「合成・分解ができる」お子さまでは、次の能力を育てたいときのスタート地点が、異なってきます。
本来、幼児期の学びでは、解答が「正しい」「間違っている」ことを第一優先にするべきではなく、
「そのお子さまの能力が、正しい方向で最大限に育つか?」
が大事なはずです。
しっかりと、能力が育っていれば、解答能力も高まります。
せっかくお子さまの大切な幼児期の学びの時間を、「串刺し解法」は無駄にしてしまいます。
小学校受験塾の中には、
「まずは、年少や年中では串刺し解法で問題が解けるようになってから、できるお子さま、または年長さんになってからカタマリ(合成・分解)で数えるようにしましょう」
というような指導をしているお教室があったり、講師がいたりします。
むしろ、このような指導がスタンダートとも言えるでしょう。
これらは本当に「幼児の将来を考えている指導法」だと思うでしょうか?
小学校受験の本番の時期に「合成・分解」で解く方法を勧めるのであれば、「串刺し解法」はなんのための解法なのでしょうか?
「後伸び」を無視した、その場その時だけ「親を一時的に安心させるための解法」ですし、例えばこの「串刺し解法」で制限時間内に間に合わないお子さまへは、
「速く串を刺して、数えられるようにしましょう」
という、アドバイスになっていないアドバイスしかできません。
このように、問題ごとに「一対一の解法を教え込む」というやり方は、能力を伸ばすどころか退化させる可能性ががありますが、残念ながら似たような事例が、幼児教育の現場でまかり通っているというのが現状です。
この構造は、小学生における筆算至上主義と似ています。
例えば「12+19」レベルの足し算を、機械的に筆算をしないと解けないような人を育てているようなものです。
少し工夫すれば暗算で導き出せそうな「12+19」という足し算を、とにかく筆算で解こうするお子さまの能力が、その後に伸びると思われるでしょうか?
積み木の数も、串刺しでしか解けないお子さまは、そこでひとつの能力が完結してしまい、他の学びに生かしにくくなってしまいます。
一度、そのような癖がついてしまったお子さまの修正は意外と時間がかかります。
なぜなら、
「小学校受験塾の先生が言っていることは正しい」
と、素直なお子さまであればあるほど、強く信じるからです。
そのような場合は、お子さまには解法自体は全否定せず、少しずつそのクセを取り除くことにしています。
積み木の数の問題だけで対処しようとせず、三方向知覚/五方向知覚、積み木の推理や、その他の合成・分解をするような多数の取り組みによって、徐々にお子さまに気づいていってもらうことができるのが、ピグマリオンの良さだとも言えます。
ピグマリオン学院 麻布十番教室

